Chào cả nhà “Nhật Ký Con Nít”! Chuyên gia Mẹo Vặt Cuộc Sống đây. Hôm nay, chúng ta sẽ cùng “khui” một bí mật toán học mà nghe qua có vẻ “cao siêu”, nhưng thực ra lại rất gần gũi với cuộc sống hàng ngày của chúng ta. Đó chính là câu hỏi: X đạo Hàm Bằng Mấy? Nghe đến “đạo hàm” có thể nhiều phụ huynh sẽ thấy hơi “ớn lạnh” nhớ lại thời đi học, còn các bé thì có lẽ vẫn còn xa lạ. Nhưng đừng lo, chúng ta sẽ cùng nhau khám phá nó một cách thật nhẹ nhàng, như đang chơi một trò chơi giải mã vậy!
Bạn có bao giờ tự hỏi, tốc độ của một chiếc xe thay đổi như thế nào theo thời gian? Hay cây non lớn nhanh hay chậm mỗi ngày? Hoặc đơn giản hơn, lượng nước trong bình tăng lên bao nhiêu khi bạn liên tục rót vào? Tất cả những câu hỏi về sự thay đổi, tốc độ biến đổi ấy đều có liên quan mật thiết đến khái niệm đạo hàm. Và việc biết x đạo hàm bằng mấy chính là một trong những viên gạch đầu tiên, là quy tắc cơ bản nhất khi chúng ta bắt đầu tìm hiểu về “ngôn ngữ” của sự thay đổi này. Hãy cùng “giải mã” nó nhé!
Hình ảnh minh họa sự thay đổi trong cuộc sống, ví dụ như cây lớn lên, nước chảy, ô tô chạy nhanh chậm, liên quan đến x đạo hàm bằng mấy
Đạo Hàm Là Gì Mà Nghe Có Vẻ Phức Tạp Thế?
Bạn có thể nghĩ đạo hàm là một thứ gì đó rất trừu tượng, chỉ dành cho các nhà toán học hay kỹ sư. Nhưng thực tế, nó chỉ là một công cụ để đo lường sự thay đổi “tức thời” của một cái gì đó.
Hãy hình dung thế này: Bạn đang đi bộ. Tốc độ trung bình của bạn trong cả quãng đường có thể là 5 km/h. Nhưng tại một khoảnh khắc cụ thể nào đó, khi bạn đang lên dốc hoặc xuống dốc, tốc độ của bạn có thể khác đi, nhanh hơn hoặc chậm hơn. Đạo hàm giúp chúng ta tính được cái tốc độ ngay tại khoảnh khắc đó, cái sự thay đổi ngay lập tức đó.
Đơn giản hơn nữa, hãy nghĩ về việc học. Hôm nay bạn học thêm được 5 từ tiếng Anh. Ngày mai bạn học thêm 7 từ. Tốc độ học từ mới của bạn đang thay đổi. Đạo hàm giúp chúng ta “chụp lại” chính xác tốc độ học của bạn ngay lúc này, hoặc tốc độ tăng trưởng chiều cao của con bạn tại tháng tuổi này. Nó là một cách để “đo nhịp đập” của sự thay đổi.
Vậy Tại Sao Lại Quan Tâm Đến “x Đạo Hàm Bằng Mấy”?
Trong toán học, “x” thường được dùng để đại diện cho một biến số nào đó, một giá trị có thể thay đổi. Ví dụ, “x” có thể là thời gian, hoặc là vị trí, hoặc là một lượng nào đó. Hàm số cơ bản nhất mà chúng ta có thể nghĩ đến là hàm số y = x.
Hàm số y = x nghĩa là gì? Nó có nghĩa là giá trị của y luôn luôn bằng giá trị của x. Nếu x là 1, thì y là 1. Nếu x là 5, thì y là 5. Nếu x tăng thêm 1 đơn vị, thì y cũng tăng thêm 1 đơn vị.
Bây giờ, hãy áp dụng ý tưởng về đạo hàm (đo lường sự thay đổi tức thời) vào hàm số đơn giản y = x này. Khi x thay đổi một chút, y thay đổi như thế nào?
Nếu x tăng từ 5 lên 6 (tăng 1 đơn vị), y cũng tăng từ 5 lên 6 (tăng 1 đơn vị).
Nếu x tăng từ 10 lên 10.1 (tăng 0.1 đơn vị), y cũng tăng từ 10 lên 10.1 (tăng 0.1 đơn vị).
Tỷ lệ thay đổi của y so với sự thay đổi của x trong hàm y = x luôn luôn là 1. Khi x thay đổi bao nhiêu, y thay đổi đúng bấy nhiêu. Cái “tốc độ thay đổi” của y so với x là một con số cố định. Và con số đó chính là câu trả lời cho câu hỏi x đạo hàm bằng mấy.
Hình ảnh minh họa đồ thị hàm số y = x là một đường thẳng, thể hiện độ dốc (slope) của đường thẳng, liên quan đến x đạo hàm bằng mấy
Câu Trả Lời Trực Tiếp: x Đạo Hàm Bằng Mấy?
Trả lời: x đạo hàm bằng mấy? Đáp án chính xác và đơn giản là 1.
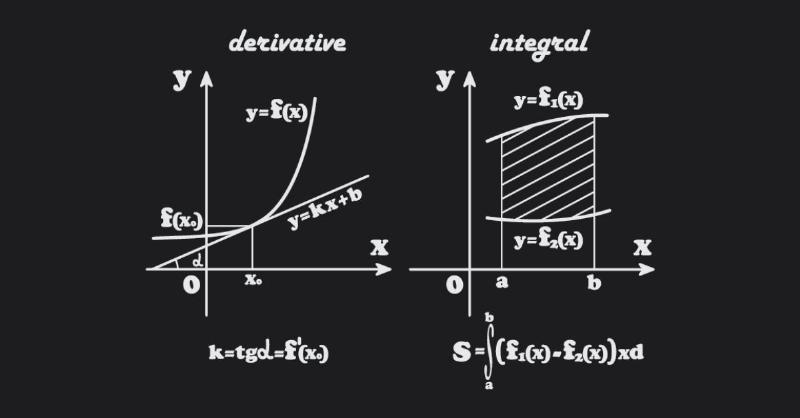
Tại sao lại là 1? Như chúng ta vừa phân tích ở trên, hàm số y = x biểu diễn một mối quan hệ tuyến tính, nghĩa là khi x thay đổi, y cũng thay đổi một cách đều đặn. Tỷ lệ thay đổi này không hề thay đổi tại bất kỳ điểm nào trên đồ thị của hàm số này (đó là một đường thẳng). Tỷ lệ thay đổi đó, hay độ dốc của đường thẳng y = x, chính là 1. Và đạo hàm đo lường chính xác cái tốc độ thay đổi tức thời này. Với hàm y = x, tốc độ thay đổi tức thời này luôn luôn là 1.
Tại Sao x Đạo Hàm Lại Là 1? Giải Thích Từ Quy Tắc Đạo Hàm Cơ Bản
Để hiểu sâu hơn vì sao x đạo hàm bằng mấy là 1, chúng ta cần làm quen với một quy tắc rất quan trọng trong đạo hàm, đó là “Quy tắc lũy thừa” (Power Rule).
Quy tắc này nói rằng: Nếu bạn có một hàm số dạng y = x^n (x mũ n), thì đạo hàm của nó sẽ là n * x^(n-1). Ký hiệu đạo hàm của y theo x thường là y’ hoặc dy/dx.
Công thức: d/dx (x^n) = n * x^(n-1)
Bây giờ, hãy áp dụng quy tắc này cho trường hợp của chúng ta: y = x.
Bạn có thể thấy rằng x chính là x mũ 1 (x^1). Tức là trong trường hợp này, n = 1.
Áp dụng công thức:
d/dx (x^1) = 1 x^(1-1)
= 1 x^0
Trong toán học, bất kỳ số nào (khác 0) mũ 0 đều bằng 1. Vì x là biến số, chúng ta giả định x khác 0 trong ngữ cảnh này (hoặc xét giới hạn khi x tiến tới 0, kết quả vẫn là 1).
Vậy:
1 x^0 = 1 1 = 1
Đó chính là lý do toán học chặt chẽ giải thích vì sao x đạo hàm bằng mấy lại bằng 1. Nó tuân theo quy tắc chung của đạo hàm cho các hàm số dạng lũy thừa.
[blockquote]Tóm lại, x đạo hàm bằng mấy là 1 vì hàm số y = x (hay y = x^1) có tốc độ thay đổi cố định là 1 tại mọi điểm. Áp dụng Quy tắc lũy thừa cơ bản trong đạo hàm, d/dx (x^1) = 1 x^(1-1) = 1 x^0 = 1 * 1 = 1.[/blockquote]Những “Viên Gạch” Toán Học Đơn Giản Khác Bên Cạnh x Đạo Hàm Bằng Mấy
Để xây dựng ngôi nhà kiến thức, chúng ta cần nhiều viên gạch. Việc hiểu x đạo hàm bằng mấy là một viên gạch quan trọng, nhưng còn những viên khác nữa cũng rất đơn giản và cần biết:
-
Đạo hàm của một hằng số (một số cố định) bằng mấy?
- Trả lời: Đạo hàm của một hằng số (ví dụ: 5, 100, -7) luôn bằng 0.
- Giải thích: Hằng số là một giá trị không thay đổi. Nếu y = 5, thì dù x có thay đổi thế nào đi nữa, y vẫn là 5. Sự thay đổi của y so với x là bằng 0. Tốc độ thay đổi bằng 0.
- Công thức: d/dx (c) = 0 (với c là hằng số)
-
*Đạo hàm của cx (một hằng số nhân với x) bằng mấy?**
- Trả lời: Đạo hàm của c*x bằng chính hằng số c đó.
- Giải thích: Hàm số y = cx. Ví dụ y = 2x. Khi x tăng 1 đơn vị, y tăng 2 đơn vị. Tốc độ thay đổi là 2. Nếu y = 5x, khi x tăng 1 đơn vị, y tăng 5 đơn vị. Tốc độ thay đổi là 5. Áp dụng quy tắc: d/dx (cx) = c d/dx(x). Vì d/dx(x) = 1 (chúng ta vừa biết x đạo hàm bằng mấy là 1), nên d/dx (cx) = c * 1 = c.
Những quy tắc đơn giản này, cùng với việc biết x đạo hàm bằng mấy là 1, chính là nền tảng để chúng ta tính đạo hàm của nhiều hàm số phức tạp hơn sau này. Nó giống như việc học bảng chữ cái và cách ghép vần trước khi đọc được một cuốn sách vậy.
Hình ảnh minh họa các quy tắc đạo hàm cơ bản nhất: đạo hàm của hằng số, đạo hàm của x, đạo hàm của cx, liên quan đến x đạo hàm bằng mấy
Áp Dụng Quy Tắc: Tính Đạo Hàm Của x Qua Từng Bước
Hãy cùng nhau “làm bài tập” nho nhỏ để thấy rõ hơn quy trình tính đạo hàm của x dựa trên Quy tắc lũy thừa. Việc này giống như học cách lắp ráp một món đồ chơi theo hướng dẫn vậy.
- Xác định hàm số: Hàm số của chúng ta là y = x.
- Viết lại hàm số dưới dạng lũy thừa: Hàm y = x có thể viết là y = x¹. Ở đây, số mũ n là 1.
- Áp dụng Quy tắc lũy thừa: Công thức là d/dx (xⁿ) = n * xⁿ⁻¹.
- Thay giá trị n=1 vào công thức: d/dx (x¹) = 1 * x¹⁻¹.
- Thực hiện phép trừ ở số mũ: 1 – 1 = 0. Ta có 1 * x⁰.
- Tính giá trị x⁰: Bất kỳ số nào mũ 0 đều bằng 1 (với x khác 0). Vậy x⁰ = 1.
- Thực hiện phép nhân còn lại: 1 * 1 = 1.
Vậy là, từng bước một, chúng ta đã chứng minh được rằng x đạo hàm bằng mấy là 1. Thật đơn giản phải không nào?
- Bước 1: Hàm số y = x.
- Bước 2: y = x¹ (n=1).
- Bước 3: Áp dụng d/dx (xⁿ) = n * xⁿ⁻¹.
- Bước 4: d/dx (x¹) = 1 * x¹⁻¹.
- Bước 5: = 1 * x⁰.
- Bước 6: x⁰ = 1.
- Bước 7: 1 * 1 = 1.
Kết quả cuối cùng: đạo hàm của x là 1.
Hình ảnh minh họa từng bước áp dụng quy tắc lũy thừa để tính đạo hàm của x bằng 1, làm rõ x đạo hàm bằng mấy
Đạo Hàm Của X Trong Đời Sống: Nơi Những Khái Niệm Trừu Tượng Trở Nên Hữu Hình
Có lẽ bạn sẽ nghĩ: “Biết x đạo hàm bằng mấy thì có ích gì trong cuộc sống hàng ngày?”. Câu trả lời là rất nhiều đấy! Tuy khái niệm toán học này ban đầu có vẻ trừu tượng, nhưng nó mô tả các hiện tượng thực tế quanh ta.
Hãy lấy ví dụ về tốc độ. Nếu quãng đường S mà một vật đi được tỉ lệ thuận với thời gian t theo công thức S = vt (với v là vận tốc không đổi), đây chính là dạng của hàm y = cx mà chúng ta đã nói (S đóng vai trò của y, t đóng vai trò của x, v đóng vai trò của c). Đạo hàm của quãng đường theo thời gian chính là vận tốc. Áp dụng quy tắc: dS/dt = d/dt (vt). Với v là hằng số, đạo hàm của t theo t (giống như x đạo hàm bằng mấy, nhưng biến là t) là 1. Vậy dS/dt = v 1 = v.
Nghĩa là, nếu bạn đi với vận tốc không đổi 50 km/h, công thức quãng đường là S = 50t. Đạo hàm của S theo t là 50. Con số 50 này chính là vận tốc của bạn tại mọi thời điểm. Tốc độ thay đổi của quãng đường chính là vận tốc!
Đây là một ví dụ đơn giản nhất cho thấy đạo hàm đo lường tốc độ thay đổi. Và việc biết x đạo hàm bằng mấy là 1 là bước đầu tiên để hiểu được cách tính đạo hàm của những hàm số phức tạp hơn mô tả các chuyển động có vận tốc thay đổi (chuyển động có gia tốc).
Hình ảnh minh họa mối liên hệ giữa quãng đường, vận tốc và đạo hàm, sử dụng ví dụ xe chạy để làm rõ ý nghĩa thực tế của đạo hàm và liên quan đến x đạo hàm bằng mấy
Mở Rộng: Đạo Hàm Của Các Hàm Số Lũy Thừa Khác
Sau khi đã nắm chắc x đạo hàm bằng mấy là 1, chúng ta có thể dễ dàng tính đạo hàm của x mũ bất kỳ bằng Quy tắc lũy thừa: d/dx (xⁿ) = n * xⁿ⁻¹.
-
x² đạo hàm bằng mấy?
- Ở đây n = 2.
- Áp dụng công thức: d/dx (x²) = 2 x²⁻¹ = 2 x¹.
- Vậy, x² đạo hàm bằng 2x.
-
x³ đạo hàm bằng mấy?
- Ở đây n = 3.
- Áp dụng công thức: d/dx (x³) = 3 x³⁻¹ = 3 x².
- Vậy, x³ đạo hàm bằng 3x².
-
x¹⁰ đạo hàm bằng mấy?
- Ở đây n = 10.
- Áp dụng công thức: d/dx (x¹⁰) = 10 x¹⁰⁻¹ = 10 x⁹.
- Vậy, x¹⁰ đạo hàm bằng 10x⁹.
Bạn thấy không? Khi đã hiểu vì sao x đạo hàm bằng mấy là 1 và nắm được Quy tắc lũy thừa, bạn có thể “giải mã” được đạo hàm của rất nhiều hàm số khác một cách dễ dàng.
Kết Nối Với Những Kiến Thức Khác: Math Là Một Hệ Thống
Việc học toán giống như việc xây dựng một tòa nhà lớn. Mỗi khái niệm mới là một tầng, một phòng, và tất cả đều liên kết với nhau bằng những viên gạch nền móng chắc chắn. Hiểu x đạo hàm bằng mấy là 1 là một trong những viên gạch nền móng ấy khi bước vào thế giới vi tích phân.
Nó cũng liên quan đến những khái niệm toán học cơ bản khác mà các con có thể đã hoặc sẽ học. Chẳng hạn, khi bé học về [công thức tính chu vi hình tròn], bé đang học cách đo lường một đại lượng cụ thể (chu vi) dựa trên một đại lượng khác (bán kính hoặc đường kính). Đó là mối quan hệ giữa các biến số. Đạo hàm là một bước tiến xa hơn, giúp chúng ta hiểu không chỉ giá trị của đại lượng đó, mà còn cả tốc độ mà nó thay đổi.
Hoặc khi con làm quen với [số la mã từ 1 tới 100], con đang học một hệ thống ký hiệu khác để biểu diễn các con số quen thuộc. Tương tự, đạo hàm là một “ngôn ngữ” mới để mô tả sự thay đổi, bổ sung cho ngôn ngữ số học và đại số truyền thống.
Hình ảnh minh họa toán học như một mạng lưới hoặc hệ thống kết nối các khái niệm khác nhau, từ số học cơ bản đến vi tích phân, làm nổi bật vị trí của đạo hàm x và mối liên hệ với các kiến thức toán học khác
Làm Thế Nào Để Giúp Con Tiếp Cận Các Khái Niệm Toán Học Trừu Tượng Như Đạo Hàm (Khi Đến Lúc)?
Với vai trò là Chuyên gia Mẹo Vặt Cuộc Sống của “Nhật Ký Con Nít”, tôi luôn muốn chia sẻ những cách để phụ huynh có thể đồng hành cùng con trên hành trình học tập. Mặc dù đạo hàm là khái niệm dành cho lứa tuổi lớn hơn, nhưng cách chúng ta tiếp cận toán học ngay từ nhỏ sẽ ảnh hưởng đến việc con có thấy nó đáng sợ hay thú vị khi gặp những khái niệm như x đạo hàm bằng mấy.
- Biến toán học thành trò chơi: Ngay từ khi con còn bé, hãy lồng ghép toán học vào các trò chơi. Ví dụ, khi con 3 tuổi, bạn có thể chơi [trò chơi cho trẻ 3 tuổi] liên quan đến đếm, nhận biết hình dạng. Điều này giúp con có cái nhìn tích cực về việc học toán.
- Liên hệ với đời sống: Luôn cố gắng chỉ cho con thấy toán học có mặt ở khắp mọi nơi: từ việc chia bánh, đếm tiền, đo đạc khi nấu ăn (giống như chuẩn bị [thực đơn cho bé 6 tháng] cần định lượng chính xác), đến việc hiểu tại sao bóng rổ lại bay theo quỹ đạo cong, hay dự đoán thời tiết.
- Tập trung vào “Tại sao”: Khi con hỏi về một khái niệm toán học nào đó, đừng chỉ đưa ra công thức hay câu trả lời. Hãy cố gắng giải thích “Tại sao” nó lại như vậy bằng ngôn ngữ đơn giản nhất, dùng các ví dụ cụ thể. Điều này giúp con hiểu sâu sắc hơn và không cảm thấy toán học là một mớ quy tắc khô khan.
- Khuyến khích sự tò mò: Hãy để con tự đặt câu hỏi, tự khám phá. Thậm chí những câu hỏi đơn giản như “Tại sao 2+2=4?” cũng là cơ hội để bạn cùng con tìm hiểu sâu hơn về bản chất của phép cộng.
- Xây dựng nền tảng vững chắc: Trước khi hiểu đạo hàm, con cần nắm vững đại số cơ bản, khái niệm về hàm số, giới hạn (một cách trực quan). Đừng đốt cháy giai đoạn.
Những Ngộ Nhận Thường Gặp Khi Mới Tiếp Cận Khái Niệm Đạo Hàm
Khi mới làm quen với đạo hàm, không ít người (cả học sinh lẫn người lớn) thường gặp phải một vài ngộ nhận. Hiểu rõ những điều này sẽ giúp chúng ta học hiệu quả hơn.
- Ngộ nhận 1: Đạo hàm chỉ là công thức khô khan.
- Thực tế: Như chúng ta đã thảo luận, đạo hàm là công cụ mạnh mẽ để mô tả sự thay đổi trong thế giới thực. Công thức chỉ là cách chúng ta tính toán nó một cách chính xác. Hãy luôn cố gắng liên hệ công thức với ý nghĩa thực tế của nó.
- Ngộ nhận 2: Đạo hàm của x là x.
- Thực tế: Câu trả lời là x đạo hàm bằng mấy là 1, không phải x. Ngộ nhận này có thể xuất phát từ việc nhầm lẫn với một phép toán khác hoặc đơn giản là chưa nắm vững Quy tắc lũy thừa.
- Ngộ nhận 3: Chỉ có hàm x mới tính được đạo hàm.
- Thực tế: Đạo hàm có thể áp dụng cho rất nhiều loại hàm số khác nhau: hàm đa thức (chứa x², x³, …), hàm lượng giác (sin x, cos x), hàm mũ, hàm logarit, và nhiều hàm phức tạp hơn nữa. Việc hiểu đạo hàm của x là bước khởi đầu.
- Ngộ nhận 4: Học đạo hàm không có ứng dụng gì.
- Thực tế: Đạo hàm có vô vàn ứng dụng trong khoa học, kỹ thuật, kinh tế, y học, vật lý, hóa học (như tính tốc độ phản ứng, liên quan đến các khái niệm như [nguyên tử khối của clo] và khối lượng chất)… Nó giúp chúng ta phân tích tối ưu hóa (tìm giá trị lớn nhất/nhỏ nhất), dự đoán xu hướng, mô hình hóa các hiện tượng tự nhiên.
Xây Dựng Nền Tảng Toán Học Vững Chắc Cho Con
Hành trình học toán của con là một cuộc phiêu lưu dài. Từ việc nhận biết các con số, hình khối đơn giản, học cách đếm, làm các phép tính cộng trừ nhân chia, rồi đến các khái niệm phức tạp hơn như phân số, số thập phân, đại số, hình học, và cuối cùng là giải tích với giới hạn, đạo hàm, tích phân.
Việc giúp con xây dựng một nền tảng vững chắc ở mỗi giai đoạn là cực kỳ quan trọng. Một nền tảng vững chắc không chỉ là thuộc làu công thức, mà là hiểu được ý nghĩa đằng sau chúng. Khi con hiểu tại sao 2 + 2 = 4 thông qua việc gộp 2 cái kẹo với 2 cái kẹo khác, con sẽ dễ dàng chấp nhận và hiểu được những khái niệm trừu tượng hơn sau này.
Tương tự, khi đến lúc con học về đạo hàm, việc con hiểu được x đạo hàm bằng mấy không chỉ là nhớ số 1, mà là hiểu rằng hàm y = x biểu thị một mối quan hệ có tốc độ thay đổi không đổi, và tốc độ đó chính là 1. Sự hiểu biết này sẽ là bệ phóng để con tiếp thu các quy tắc đạo hàm khác và thấy được vẻ đẹp logic, ứng dụng của toán học.
Hãy kiên nhẫn đồng hành cùng con, biến việc học toán thành những khám phá thú vị. Sử dụng các mẹo vặt cuộc sống để lồng ghép các khái niệm toán học một cách tự nhiên nhất có thể.
Câu Hỏi Thường Gặp Về X Đạo Hàm Bằng Mấy
Để tối ưu hóa cho tìm kiếm bằng giọng nói và giúp bạn dễ dàng tìm thấy thông tin, chúng ta sẽ tổng hợp lại một số câu hỏi thường gặp về chủ đề này.
- Đạo hàm của x mũ 1 là bao nhiêu?
- Trả lời: Đạo hàm của x mũ 1, tức là đạo hàm của x, là 1. Đây là kết quả trực tiếp từ Quy tắc lũy thừa d/dx(xⁿ) = nxⁿ⁻¹ với n=1.
- Làm thế nào để tính đạo hàm của x?
- Trả lời: Để tính đạo hàm của x, bạn áp dụng Quy tắc lũy thừa cho trường hợp x = x¹. Số mũ là 1, vậy đạo hàm là 1 x¹⁻¹ = 1 x⁰ = 1 * 1 = 1.
- Tại sao đạo hàm của x lại bằng 1?
- Trả lời: Đạo hàm của x bằng 1 vì hàm số y = x biểu thị một mối quan hệ tuyến tính với độ dốc (tốc độ thay đổi) cố định là 1. Tức là, khi x thay đổi một đơn vị, y cũng thay đổi một đơn vị.
- Quy tắc đạo hàm cơ bản cho x là gì?
- Trả lời: Quy tắc đạo hàm cơ bản cho x là d/dx(x) = 1. Đây là một trong những quy tắc đạo hàm nền tảng nhất, suy ra từ Quy tắc lũy thừa tổng quát.
- Đạo hàm của hàm số y=x là gì?
- Trả lời: Đạo hàm của hàm số y=x là y’ = 1. Ký hiệu dy/dx cũng có nghĩa tương tự, và dy/dx = 1.
- X’ (x phẩy) trong toán học nghĩa là gì?
- Trả lời: X’ hoặc x’ thường được dùng để ký hiệu đạo hàm của x theo một biến khác (thường là thời gian t), hoặc đôi khi là đạo hàm của một hàm theo biến x đó. Tuy nhiên, nếu xét đạo hàm của hàm f(x)=x theo biến x, thì f'(x)=1.
- Đạo hàm của x theo dx là gì?
- Trả lời: Đạo hàm của x theo dx (thường ký hiệu là d/dx(x)) chính là việc tính tốc độ thay đổi của x so với sự thay đổi của x. Kết quả là 1.
- Trong công thức d/dx(x) = 1, dx nghĩa là gì?
- Trả lời: dx trong ký hiệu d/dx(x) biểu thị một sự thay đổi rất nhỏ của biến x. Cả cụm d/dx là ký hiệu cho phép toán đạo hàm theo biến x.
- Đạo hàm của x khác 0 không?
- Trả lời: Có, đạo hàm của x là 1, và 1 khác 0. Điều này cho thấy khi x thay đổi, giá trị của hàm y=x có thay đổi, với tốc độ là 1.
Hình ảnh minh họa các ứng dụng thực tế của đạo hàm trong các lĩnh vực khác nhau như vật lý (tốc độ, gia tốc), kinh tế (lợi nhuận cận biên), kỹ thuật, làm nổi bật sự hữu ích của khái niệm này bắt nguồn từ những điều cơ bản như x đạo hàm bằng mấy
Kết Luận: Từ X Đạo Hàm Bằng Mấy Đến Hiểu Về Sự Thay Đổi
Vậy là chúng ta đã cùng nhau “giải mã” câu hỏi x đạo hàm bằng mấy. Đáp án đơn giản là 1, nhưng đằng sau con số 1 đó là cả một ý nghĩa về sự thay đổi, về tốc độ, và là nền tảng cho nhiều khái niệm toán học phức tạp hơn.
Việc hiểu được những điều cơ bản này không chỉ giúp chúng ta giải quyết các bài toán, mà còn giúp chúng ta có thêm một “công cụ” để quan sát và hiểu thế giới xung quanh – thế giới luôn vận động và thay đổi không ngừng.
Đối với các bậc phụ huynh, hy vọng bài viết này đã giúp bạn ôn lại một chút kiến thức toán học và quan trọng hơn là có thêm góc nhìn về cách truyền tình yêu và sự tò mò với toán học cho con cái. Hãy bắt đầu từ những điều đơn giản nhất, liên hệ với cuộc sống hàng ngày, và kiên nhẫn giải thích “Tại sao”.
Hãy thử áp dụng những “mẹo” nhỏ này khi cùng con học toán. Đừng ngại ngần chia sẻ trải nghiệm của bạn ở phần bình luận dưới đây nhé! Hẹn gặp lại trong những bài viết mẹo vặt cuộc sống thú vị khác trên “Nhật Ký Con Nít”!