Chào mừng cả nhà đến với “Nhật Ký Con Nít”! Tôi là Chuyên gia Mẹo Vặt Cuộc Sống đây, và hôm nay, chúng ta sẽ cùng nhau “khám phá” một bí mật toán học tưởng chừng phức tạp nhưng lại cực kỳ hữu ích trong cuộc sống hàng ngày: chính là [công thức tính diện tích tam giác]. Tại sao lại gọi đây là “mẹo vặt”? Bởi vì hiểu rõ công thức này không chỉ giúp con bạn học tốt Toán hơn, mà còn mở ra vô vàn ứng dụng thực tế đầy thú vị, biến việc học thành một cuộc phiêu lưu. Chỉ cần nắm vững vài bước đơn giản, việc tìm ra diện tích của bất kỳ hình tam giác nào sẽ trở nên dễ như ăn kẹo! Vậy thì, Công Thức Tính S Tam Giác cụ thể là gì và làm thế nào để áp dụng nó một cách hiệu quả nhất? Hãy cùng lật mở từng trang bí kíp nhé!
Công Thức Tính S Tam Giác Cơ Bản Nhất Là Gì?
Bạn hỏi công thức tính S (diện tích) tam giác cơ bản nhất là gì?
Công thức tính diện tích tam giác phổ biến và dễ nhớ nhất là lấy nửa tích của độ dài cạnh đáy và chiều cao tương ứng với cạnh đáy đó.
Để dễ hình dung, bạn hãy tưởng tượng một hình tam giác đặt trên mặt bàn. Một trong ba cạnh của tam giác được chọn làm “cạnh đáy”. “Chiều cao” tương ứng là đoạn thẳng vuông góc kẻ từ đỉnh đối diện xuống cạnh đáy (hoặc đường thẳng chứa cạnh đáy đó). Công thức được biểu diễn như sau:
Diện tích = (Cạnh đáy x Chiều cao) / 2
Hay viết gọn hơn: S = (a * h) / 2
Trong đó:
- S là diện tích của tam giác.
- a là độ dài cạnh đáy được chọn.
- h là chiều cao tương ứng với cạnh đáy a.
Công thức này giống như việc bạn chia đôi một hình chữ nhật hoặc hình bình hành vậy đó! Nếu bạn vẽ một hình chữ nhật có chiều dài bằng cạnh đáy tam giác và chiều rộng bằng chiều cao tam giác, bạn sẽ thấy tam giác của chúng ta chỉ chiếm đúng một nửa diện tích của hình chữ nhật đó. Thật kỳ diệu phải không nào? Đây chính là “mẹo” giúp bạn ghi nhớ công thức tính s tam giác này mãi mãi!
Tại Sao Lại Là “Chia Hai”?
Tại sao trong công thức tính s tam giác lại luôn có phần “chia hai”?
Phép chia hai trong công thức tính diện tích tam giác xuất phát từ mối liên hệ giữa tam giác và hình chữ nhật (hoặc hình bình hành).
Hãy thử tưởng tượng nhé: bạn có một hình chữ nhật. Nếu bạn kẻ một đường chéo từ một góc tới góc đối diện, bạn sẽ chia hình chữ nhật đó thành hai hình tam giác vuông có diện tích bằng nhau. Diện tích của hình chữ nhật là Chiều dài x Chiều rộng. Vì tam giác vuông là một nửa hình chữ nhật, nên diện tích của nó là (Chiều dài x Chiều rộng) / 2.
Mở rộng ra với tam giác bất kỳ: bạn luôn có thể “nhốt” một tam giác vào trong một hình chữ nhật hoặc hình bình hành sao cho tam giác đó chiếm chính xác một nửa diện tích của hình lớn hơn. Chiều dài của hình lớn sẽ là cạnh đáy tam giác, và chiều rộng (hoặc chiều cao) của hình lớn sẽ là chiều cao tương ứng của tam giác. Vì vậy, diện tích tam giác luôn bằng (Cạnh đáy x Chiều cao) / 2. Nó giống như một quy luật tự nhiên của hình học vậy đó! Nắm được gốc rễ này, bạn sẽ thấy công thức tính s tam giác thật logic và dễ nhớ hơn rất nhiều.
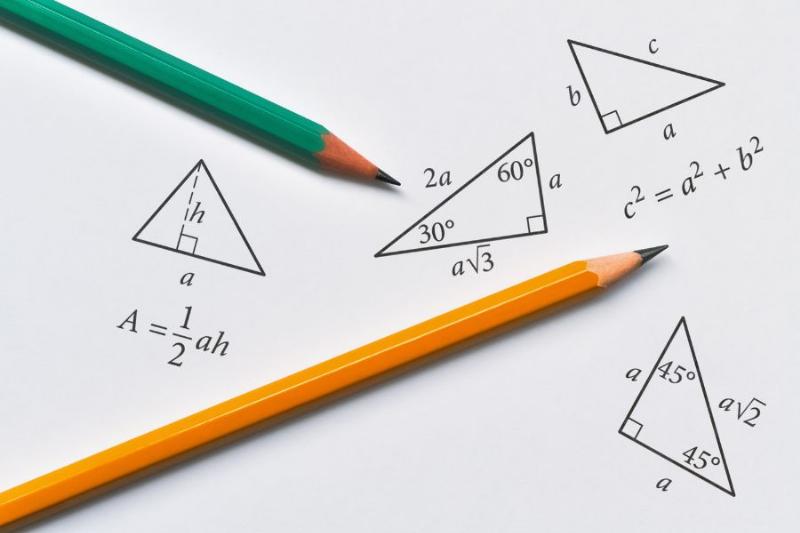Hinh minh hoa cong thuc tinh dien tich tam giac co ban voi canh day va chieu cao
Các Loại Tam Giác Đặc Biệt – Có Công Thức Nào Riêng Không?
Có những loại tam giác đặc biệt nào và liệu có công thức tính S tam giác riêng cho chúng không?
Về cơ bản, công thức tính s tam giác S = (a * h) / 2 vẫn áp dụng được cho mọi loại tam giác, dù là tam giác vuông, tam giác cân hay tam giác đều. Tuy nhiên, với những loại tam giác đặc biệt này, đôi khi chúng ta có thể tìm ra những “đường tắt” hoặc cách tính nhanh hơn dựa vào các đặc điểm riêng của chúng.
Tam Giác Vuông: “Anh Bạn Thân” Của Hình Chữ Nhật
Với tam giác vuông, một trong hai cạnh góc vuông có thể được coi là cạnh đáy, và cạnh góc vuông còn lại chính là chiều cao tương ứng! Thật tiện lợi phải không?
Vì thế, công thức tính s tam giác vuông trở nên siêu đơn giản:
S = (Cạnh góc vuông 1 * Cạnh góc vuông 2) / 2
Đây là trường hợp dễ áp dụng nhất của công thức cơ bản, vì bạn không cần phải kẻ thêm đường cao nữa. Chỉ cần đo độ dài hai cạnh “ôm lấy” góc vuông là xong!
Tam Giác Cân: Đối Xứng Và Đẹp Đẽ
Tam giác cân có hai cạnh bên bằng nhau. Đường cao kẻ từ đỉnh tạo bởi hai cạnh bên này xuống cạnh đáy cũng đồng thời là đường trung tuyến và đường phân giác. Điều này có nghĩa là nó chia cạnh đáy thành hai phần bằng nhau và chia góc ở đỉnh thành hai góc bằng nhau.
Để tính diện tích tam giác cân, bạn vẫn dùng công thức S = (a * h) / 2. Vấn đề là làm sao tìm được chiều cao h nếu chỉ biết độ dài các cạnh? Lúc này, định lý Pytago sẽ là “trợ thủ” đắc lực của bạn. Nếu gọi cạnh đáy là ‘a’ và cạnh bên là ‘b’, chiều cao ‘h’ sẽ tạo thành một tam giác vuông với nửa cạnh đáy (a/2) và cạnh bên ‘b’.
Theo Pytago: h² + (a/2)² = b²
Suy ra: h = √(b² – (a/2)²)
Sau khi tính được h, bạn lại áp dụng công thức cơ bản để tính S. Khá tiện lợi khi bạn cần [tính diện tích tam giác cân] mà không có thông tin về chiều cao trực tiếp.
Tam Giác Đều: Hoàn Hảo Mọi Mặt
Tam giác đều có ba cạnh bằng nhau và ba góc bằng nhau (đều là 60 độ). Nó là trường hợp đặc biệt nhất của tam giác cân. Đường cao trong tam giác đều cũng là đường trung tuyến, phân giác, đường trung trực… và ba đường cao đều bằng nhau!
Nếu gọi độ dài cạnh của tam giác đều là ‘a’, chiều cao ‘h’ của tam giác đều có thể tính nhanh bằng công thức:
h = a * √3 / 2
Từ đó, công thức tính s tam giác đều cũng có thể rút gọn lại thành một công thức chỉ phụ thuộc vào độ dài cạnh ‘a’:
S = (a h) / 2 = (a (a √3 / 2)) / 2 = (a² √3) / 4
Công thức này giúp bạn [công thức tính nhanh diện tích tam giác đều] chỉ trong nháy mắt nếu biết độ dài cạnh. Nắm vững những công thức “tốc hành” này sẽ giúp việc giải toán của con trở nên nhẹ nhàng và nhanh chóng hơn bao giờ hết!
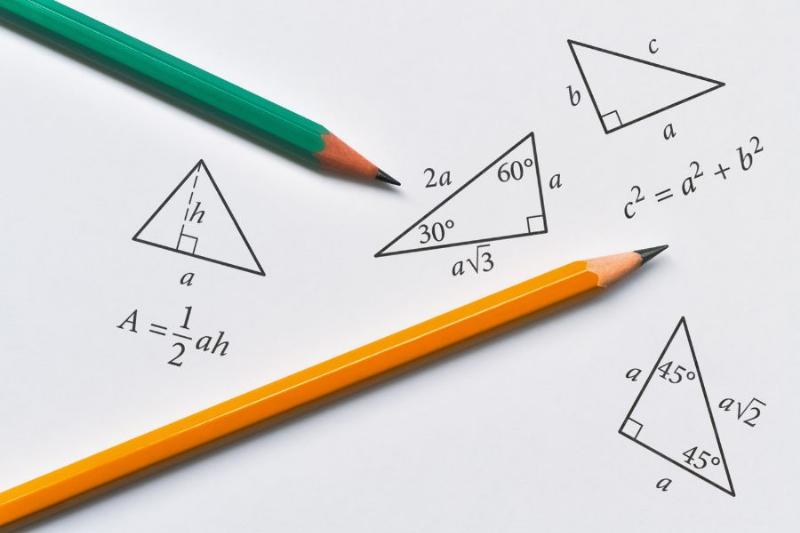Minh hoa cac loai tam giac vuong can deu va cong thuc rieng
Áp Dụng Công Thức Tính S Tam Giác Trong Cuộc Sống Thực?
Bạn có thắc mắc liệu công thức tính s tam giác chỉ gói gọn trong sách vở hay có thể áp dụng vào cuộc sống thực?
Ồ, chắc chắn rồi! Toán học không chỉ là những con số khô khan, nó ẩn chứa trong mọi thứ xung quanh ta. Công thức tính s tam giác là một ví dụ tuyệt vời về việc toán học có thể là một “mẹo vặt” cực hữu ích trong đời sống hàng ngày của cả gia đình.
Thiết Kế Và Trang Trí Nhà Cửa
Bạn muốn lát gạch một khoảng sân hình tam giác? Hay cắt một tấm thảm hình tam giác để kê dưới chiếc bàn góc? Để biết cần mua bao nhiêu vật liệu, bạn cần tính diện tích của khu vực đó. Nắm vững công thức tính s tam giác giúp bạn tính toán chính xác, tránh lãng phí tiền bạc và vật liệu. Ba mẹ có thể cùng con đo đạc, tính toán ngay trong chính ngôi nhà của mình, biến việc học thành một hoạt động gia đình vui vẻ.
Làm Vườn Hay Trồng Cây
Gia đình bạn có một khoảng đất nhỏ hình tam giác muốn làm vườn? Để biết cần bao nhiêu đất, hạt giống, hay phân bón cho vừa đủ, bạn cần tính diện tích. Đây là lúc công thức tính s tam giác phát huy tác dụng! Việc này không chỉ giúp con ôn lại bài mà còn hiểu được ý nghĩa thực tế của những gì học ở trường.
May Vá, Thủ Công Và Các Dự Án Sáng Tạo
Bạn muốn may một chiếc gối hình tam giác, cắt vải để ghép thành hình trang trí, hay làm một mô hình chóp tam giác? Biết cách tính diện tích tam giác giúp bạn đo đạc chính xác lượng vải, giấy, hoặc vật liệu khác cần dùng. Các bé lớn hơn có thể tự tính toán phần vật liệu mình cần cho dự án thủ công, rèn luyện tính độc lập và kỹ năng giải quyết vấn đề.
Hiểu Về Các Công Trình Kiến Trúc
Tại sao mái nhà thường có hình tam giác? Tại sao các cây cầu, tháp Eiffel lại sử dụng rất nhiều cấu trúc hình tam giác? Hình tam giác có tính ổn định cao trong kỹ thuật. Việc hiểu về diện tích tam giác giúp chúng ta phần nào hiểu được cách các kỹ sư tính toán sức chịu lực và tối ưu vật liệu cho các công trình. Đây là một góc nhìn thú vị giúp con yêu thích môn Toán và Vật lý hơn.
Như bạn thấy đấy, công thức tính s tam giác không chỉ để làm bài tập về nhà. Nó là một công cụ nhỏ nhưng mạnh mẽ, giúp chúng ta hiểu và tương tác với thế giới xung quanh một cách hiệu quả hơn. Hãy cùng con tìm kiếm những “tam giác” trong nhà và áp dụng công thức này ngay hôm nay nhé! Nó đơn giản như việc tìm hiểu [công thức tính chu vi hình tròn] vậy đó, đều là những kiến thức cơ bản nhưng có vô vàn ứng dụng!
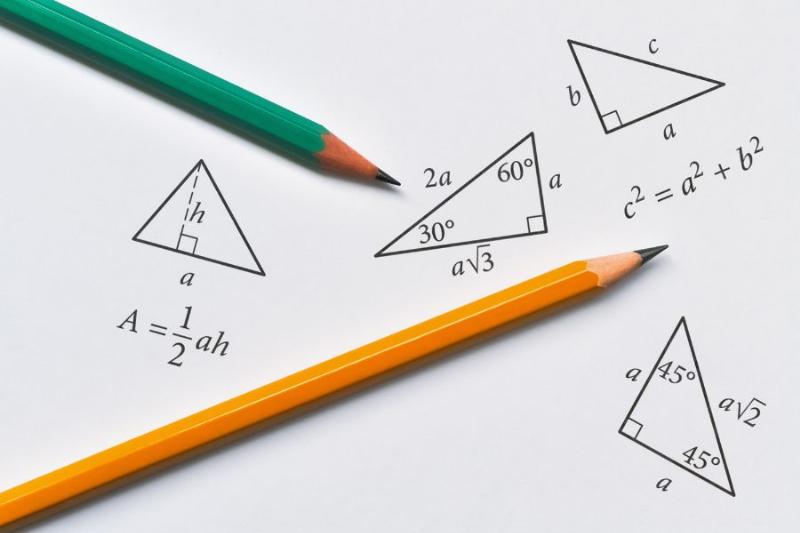Hinh minh hoa cac ung dung thuc te cua cong thuc tinh S tam giac
Làm Sao Để Con Dễ Dàng Nắm Vững Công Thức Tính S Tam Giác?
Làm thế nào để giúp con bạn, những “nhà thám hiểm toán học” tí hon, dễ dàng nắm vững công thức tính s tam giác?
Biến việc học thành trò chơi và kết nối nó với cuộc sống thực là “mẹo vặt” hiệu quả nhất.
Bắt Đầu Bằng Hình Ảnh Trực Quan
Trẻ em học tốt nhất thông qua hình ảnh và hoạt động thực tế. Thay vì chỉ đưa công thức khô khan, hãy vẽ hoặc cắt giấy thành hình tam giác. Cùng con xác định cạnh đáy và vẽ đường cao tương ứng. Sau đó, thử “biến hình” tam giác đó thành hình chữ nhật hoặc hình bình hành để con thấy mối liên hệ và hiểu tại sao lại chia hai.
Sử Dụng Các Ví Dụ “Ngon Lành”
Cắt một chiếc bánh pizza hoặc một chiếc bánh ngọt hình tròn thành các lát tam giác. Cùng con tính diện tích một lát bánh. Hoặc sử dụng một miếng dưa hấu cắt hình tam giác. Những ví dụ gần gũi, thậm chí có thể ăn được, sẽ khiến bài học trở nên hấp dẫn hơn nhiều.
“Săn Lùng” Hình Tam Giác Xung Quanh Nhà
Tổ chức một “cuộc săn lùng” hình tam giác quanh nhà hoặc khi đi dạo. Mái nhà, biển báo giao thông, một chiếc khăn gấp, cánh buồm của chiếc thuyền đồ chơi… Có vô số hình tam giác ẩn mình. Sau khi tìm thấy, hãy cùng con ước lượng cạnh đáy và chiều cao (hoặc đo đạc nếu có thể) và thử áp dụng công thức tính s tam giác để tính diện tích của chúng.
Biến Bài Tập Thành Thử Thách Nhỏ
Thay vì coi bài tập là nghĩa vụ, hãy biến chúng thành những thử thách nhỏ. Ví dụ: “Hôm nay chúng ta sẽ là kỹ sư, thử tính diện tích ‘mảnh đất’ hình tam giác này để xây ‘nhà’ nhé!” Việc tạo ra một bối cảnh hoặc câu chuyện sẽ kích thích sự hứng thú của con.
Kiên Nhẫn Và Khuyến Khích
Toán học có thể là thử thách với một số trẻ. Hãy kiên nhẫn giải thích lại khi con chưa hiểu và luôn động viên, khen ngợi sự cố gắng của con, dù kết quả ban đầu chưa hoàn hảo. Việc tạo ra môi trường học tập tích cực quan trọng hơn nhiều so với việc con giải đúng bài tập ngay lập tức.
Cô Lan, một giáo viên Toán Tiểu học với hơn 20 năm kinh nghiệm, chia sẻ: > “Điều quan trọng nhất khi dạy trẻ các khái niệm toán học là phải làm cho chúng trở nên ‘sống động’ và gần gũi. Thay vì chỉ nhìn vào sách giáo khoa, hãy đưa toán học vào gian bếp, vào khu vườn, hay vào những món đồ chơi của con. Khi trẻ thấy được ứng dụng thực tế của công thức tính s tam giác, chúng sẽ không còn cảm thấy e ngại mà trái lại, sẽ tò mò và muốn khám phá sâu hơn.”
Bên cạnh việc học tập, đừng quên rằng sự cân bằng giữa học và chơi là chìa khóa cho sự phát triển toàn diện của trẻ. Sau những giờ phút “vật lộn” với các con số và hình khối, việc dành thời gian cho những hoạt động thư giãn như đọc sách, chơi đùa, hay thậm chí là [đọc thơ cho bé ngủ ngon] sẽ giúp con tái tạo năng lượng và sẵn sàng cho những thử thách tiếp theo.
Ví Dụ Minh Họa Cách Áp Dụng Công Thức Tính S Tam Giác
Để giúp ba mẹ và các bé hình dung rõ hơn, chúng ta cùng làm một vài ví dụ đơn giản về cách áp dụng công thức tính s tam giác nhé.
Ví dụ 1: Tính diện tích một mảnh vườn hình tam giác
Gia đình bạn có một mảnh vườn nhỏ hình tam giác. Cạnh dài nhất của mảnh vườn (chọn làm cạnh đáy) đo được là 5 mét. Chiều cao từ đỉnh đối diện xuống cạnh đáy này đo được là 3 mét. Hỏi diện tích mảnh vườn là bao nhiêu mét vuông?
- Bước 1: Xác định các thông số đã biết.
- Cạnh đáy (a) = 5 mét
- Chiều cao tương ứng (h) = 3 mét
- Bước 2: Áp dụng công thức tính s tam giác cơ bản: S = (a * h) / 2
- Bước 3: Thay số vào công thức và tính toán.
- S = (5 * 3) / 2
- S = 15 / 2
- S = 7.5
- Kết luận: Diện tích mảnh vườn hình tam giác là 7.5 mét vuông.
Thật đơn giản phải không nào?
Ví dụ 2: Tính diện tích một miếng vải tam giác vuông
Bạn có một miếng vải hình tam giác vuông để may cờ. Hai cạnh góc vuông của miếng vải có độ dài lần lượt là 40 cm và 60 cm. Tính diện tích miếng vải.
- Bước 1: Nhận dạng đây là tam giác vuông. Hai cạnh góc vuông chính là cạnh đáy và chiều cao tương ứng.
- Bước 2: Xác định các thông số.
- Cạnh góc vuông 1 (coi là đáy a) = 40 cm
- Cạnh góc vuông 2 (coi là chiều cao h) = 60 cm
- Bước 3: Áp dụng công thức tính s tam giác vuông: S = (Cạnh góc vuông 1 * Cạnh góc vuông 2) / 2
- Bước 4: Thay số và tính toán.
- S = (40 * 60) / 2
- S = 2400 / 2
- S = 1200
- Kết luận: Diện tích miếng vải hình tam giác vuông là 1200 centimét vuông.
Các bé có thể thực hành ngay với các đồ vật hình tam giác có sẵn trong nhà mình, ví dụ như một chiếc ê-ke, một miếng ghép hình, hay thậm chí là một lát bánh mì cắt hình tam giác.
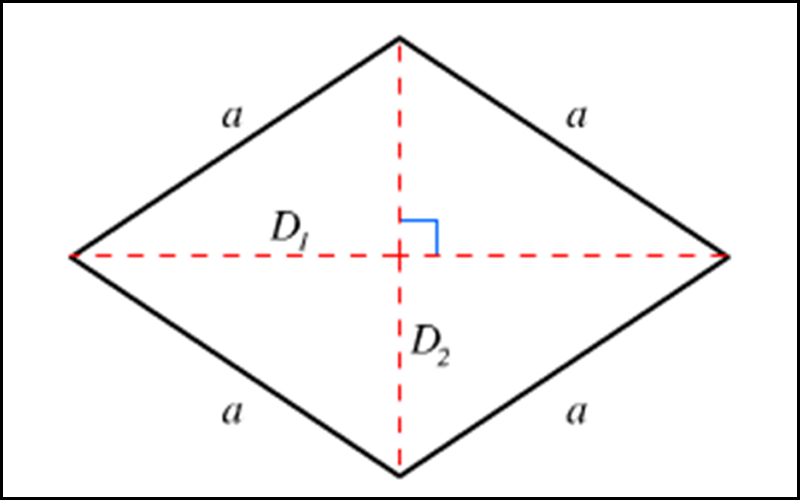Hinh minh hoa mot vi du tinh dien tich tam giac voi so lieu cu the
Ngoài Công Thức Cơ Bản, Còn Cách Nào Khác Để Tính S Tam Giác Không?
Liệu ngoài công thức tính s tam giác S = (a * h) / 2, còn cách nào khác để tính diện tích tam giác không, đặc biệt khi không biết chiều cao?
Có chứ! Toán học luôn có nhiều cách để giải quyết một vấn đề. Khi bạn không có thông tin về chiều cao nhưng biết độ dài ba cạnh của tam giác, Định lý Heron (hay còn gọi là công thức Heron) sẽ là “vị cứu tinh” của bạn.
Công Thức Heron: Khi Chỉ Biết Độ Dài Ba Cạnh
Giả sử tam giác có ba cạnh là a, b, và c.
Đầu tiên, bạn cần tính “nửa chu vi” của tam giác, ký hiệu là p.
p = (a + b + c) / 2
Sau đó, áp dụng công thức Heron để tính diện tích S:
S = √[p (p – a) (p – b) * (p – c)]
Trong đó:
- S là diện tích tam giác.
- a, b, c là độ dài ba cạnh của tam giác.
- p là nửa chu vi tam giác.
Công thức này trông có vẻ phức tạp hơn công thức tính s tam giác cơ bản, nhưng nó cực kỳ hữu ích khi bạn chỉ có thông tin về độ dài các cạnh. Ví dụ, khi bạn cần tính diện tích một mảnh đất hình tam giác mà việc đo chiều cao gặp khó khăn. Đây là một công thức nâng cao hơn, phù hợp với các bạn học sinh lớn hơn một chút, nhưng việc giới thiệu sớm cho con biết về sự tồn tại của nó cũng rất tốt, khơi gợi sự tò mò về toán học.
Công Thức Dùng Sin Góc Giữa Hai Cạnh
Một cách khác để tính diện tích tam giác là sử dụng công thức liên quan đến lượng giác, áp dụng khi bạn biết độ dài hai cạnh và góc xen giữa hai cạnh đó.
S = (1/2) a b * sin(C)
Trong đó:
- S là diện tích tam giác.
- a và b là độ dài hai cạnh bất kỳ của tam giác.
- C là góc xen giữa hai cạnh a và b.
Công thức này thường được học ở cấp trung học, nhưng nó cho thấy sự đa dạng của các phương pháp tính toán trong toán học. Nó cũng là một lời nhắc nhở rằng công thức tính s tam giác cơ bản (a*h/2) là nền tảng, nhưng còn nhiều con đường khác để đi đến đích!
Việc biết nhiều cách tiếp cận giúp chúng ta linh hoạt hơn trong việc giải quyết các bài toán trong sách vở cũng như trong cuộc sống thực tế. Nó giống như việc bạn biết nhiều “mẹo vặt” vậy đó, mỗi mẹo phù hợp với một tình huống khác nhau.
Lưu Ý Quan Trọng Khi Áp Dụng Công Thức Tính S Tam Giác
Khi giúp con học và áp dụng công thức tính s tam giác, ba mẹ cần lưu ý những điểm gì để tránh nhầm lẫn?
Để việc tính toán chính xác và suôn sẻ, hãy ghi nhớ vài điều nhỏ nhưng quan trọng nhé:
Đảm Bảo Đơn Vị Đo Lường Nhất Quán
Đây là lỗi sai rất phổ biến! Khi tính diện tích, tất cả các độ dài (cạnh đáy, chiều cao, các cạnh khác) phải cùng một đơn vị đo lường. Nếu cạnh đáy đo bằng mét, chiều cao cũng phải là mét. Không thể lấy mét nhân với centimet được nhé! Nếu các đơn vị khác nhau, phải đổi về cùng một đơn vị trước khi tính toán.
Xác Định Chính Xác Chiều Cao Tương Ứng
Nhớ rằng chiều cao luôn phải vuông góc với cạnh đáy được chọn. Đường cao có thể nằm bên trong tam giác (với tam giác nhọn), trùng với một cạnh (với tam giác vuông), hoặc nằm bên ngoài tam giác (với tam giác tù). Quan trọng là nó phải vuông góc với cạnh đáy (hoặc đường thẳng kéo dài của cạnh đáy). Việc xác định đúng “cặp đôi” cạnh đáy – chiều cao là chìa khóa để áp dụng đúng công thức tính s tam giác.
Hiểu Rõ Ý Nghĩa Của “Diện Tích”
Diện tích là phần mặt phẳng mà hình tam giác “chiếm chỗ”. Đơn vị của diện tích luôn là đơn vị đo chiều dài bình phương (ví dụ: cm², m², km²…). Nhắc nhở con ghi đúng đơn vị vào kết quả cuối cùng là một thói quen tốt.
Không Ngại Vẽ Hình
Với các bài toán phức tạp hơn, hoặc khi con chưa quen, hãy khuyến khích con vẽ hình tam giác ra giấy. Việc trực quan hóa giúp con dễ dàng xác định cạnh đáy, chiều cao, và tránh nhầm lẫn. Vẽ hình giống như một “mẹo” giúp bộ não sắp xếp thông tin tốt hơn vậy.
Thực Hành Thường Xuyên
Giống như bất kỳ kỹ năng nào khác, việc nắm vững công thức tính s tam giác đòi hỏi thực hành. Ba mẹ có thể ra các bài tập nhỏ, hoặc lồng ghép vào các hoạt động hàng ngày như đã gợi ý ở trên. “Học đi đôi với hành” luôn là nguyên tắc vàng!
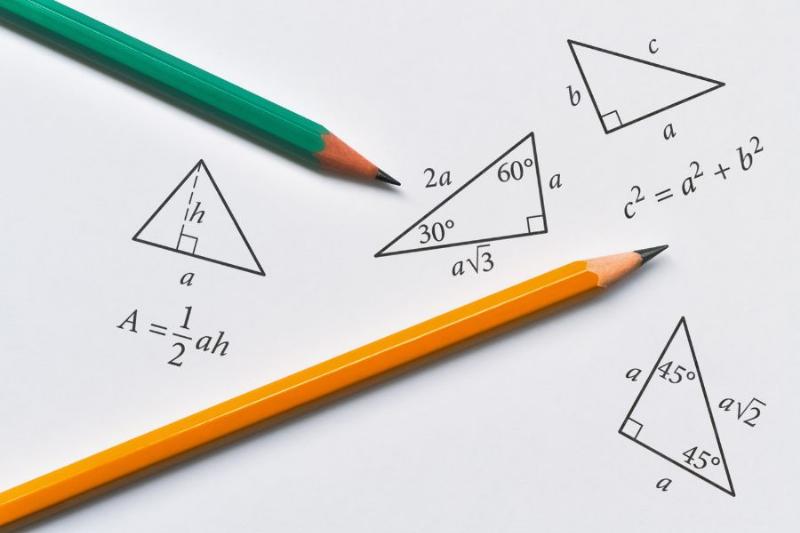Minh hoa hoat dong thuc hanh tinh dien tich tam giac
Kết Luận: Nắm Vững Công Thức Tính S Tam Giác – Mẹo Vặt Nhỏ, Lợi Ích Lớn!
Vậy là chúng ta đã cùng nhau “giải mã” công thức tính s tam giác – một kiến thức toán học cơ bản nhưng lại có vô vàn ứng dụng thực tế trong cuộc sống hàng ngày của gia đình. Từ việc tính diện tích mảnh vườn, cắt vải may vá, cho đến việc hiểu hơn về các công trình kiến trúc vĩ đại, công thức S = (a * h) / 2 luôn là người bạn đồng hành đáng tin cậy.
Việc giúp con bạn nắm vững công thức này không chỉ là để đạt điểm cao trong môn Toán, mà quan trọng hơn, là trang bị cho con một kỹ năng giải quyết vấn đề và một góc nhìn mới về thế giới xung quanh. Hãy biến việc học toán thành những giờ phút vui vẻ, khám phá cùng con, thông qua các trò chơi, ví dụ thực tế và sự kiên nhẫn, động viên từ phía ba mẹ.
Đừng ngại thử nghiệm, đừng ngại sai lầm. Quan trọng là cả nhà cùng nhau học hỏi và tiến bộ. Hãy bắt đầu ngay hôm nay bằng cách tìm một vật hình tam giác gần nhất và cùng con thử áp dụng công thức tính s tam giác xem sao nhé! Chắc chắn bạn sẽ thấy rằng, mẹo vặt toán học này không hề “khó nhằn” chút nào, mà trái lại, nó mở ra cánh cửa đến với thế giới của những con số và hình khối đầy thú vị!